GUGA的使用其实是相当的广泛的，之前本人一直使用的GAMESS，以及现在的MOCAS里面，都有的。可以说GUGA类的CI（组态相互作用方法）是一种很高效方法，尤其是在截断CI方法里面。后来，在MRCI里面也有使用，国内的西北大学研究组在这方面也做了很多的工作。虽然个人认为GUGA不如IC-MRCI简单方便（额… 起码入门不需要画图辅助啊），而且目前后者的发展势头也是猛于前者的。

OK，言归正传。让我们来看一下GUGA是怎样构建CI的行列式的。这里使用sto-3g基组下面H2o的例子，没有考虑对称性。该体系有5个alpha电子对应在7个alpha轨道上；5个beta电子对应于7个beta轨道上。考虑Sz=0的FULLCI行列式构建。

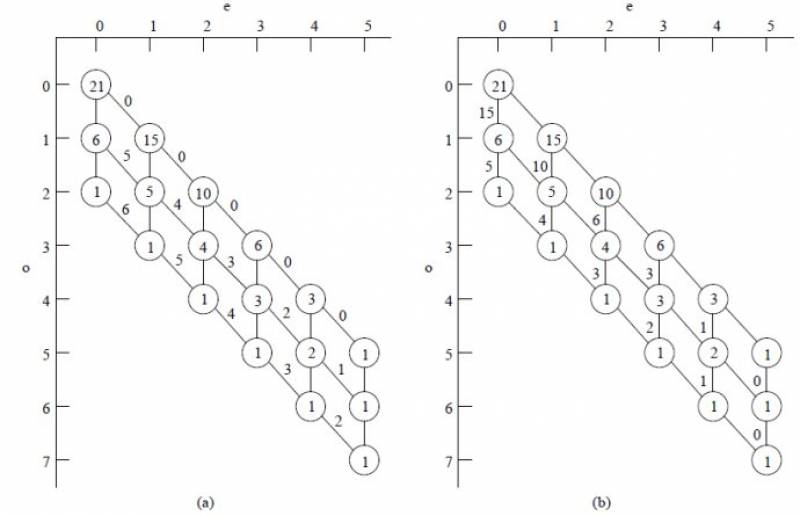
• 1） 第一步，画出图。其中，横坐标为电子数e，纵坐标为轨道数o，坐标从零开始记。横纵坐标相交处记为x(e,o)
• 2） 起点为x(0,0)处点，终点嘛为x(5,7)处。FCI下面嘛，图形简单：然后x(0,0)处对角线连接到x(5,5)处；x(5,7)处反向对角线连接到x(0,2)处。其余点自行补全
• 3） 将所有的最下以及最右（→_→）的x标记为1（lexical ordering）,然后其余的x(e,o)的值由x(e,o+1)+x(e+1,o+1)获得。
• 4） 然后就是从x(0,0)走到x(5,7)了。此处的话，会有两种表述方法
  • a) 假设从x（0,0）开始，对角线方向行走代表下一点有电子占据，比如（x(0,0)→x(1,1)）代表在x(1,1)即轨道1处有电子占据（行走的弧记为Y1(0,0)）；直接往下走代表轨道1没有电子占据,行走的弧记为Y0(0,0)。同时，所有的Y0弧记为0（图中直接没写了），所有的Y1(e,o)值为 Y1(e,o)=x(e + 1, o + 1) + x(e + 1, o) + … + x(e + 1, e + 1) 【注意坐标】
  • b）走法的意义与 a)相同，但是Y的标记与 a)相反。即所有的对角线Y（即为Y1）标记为空值，Y0为 Y0(e,o)=x(e + 1, o + 1)

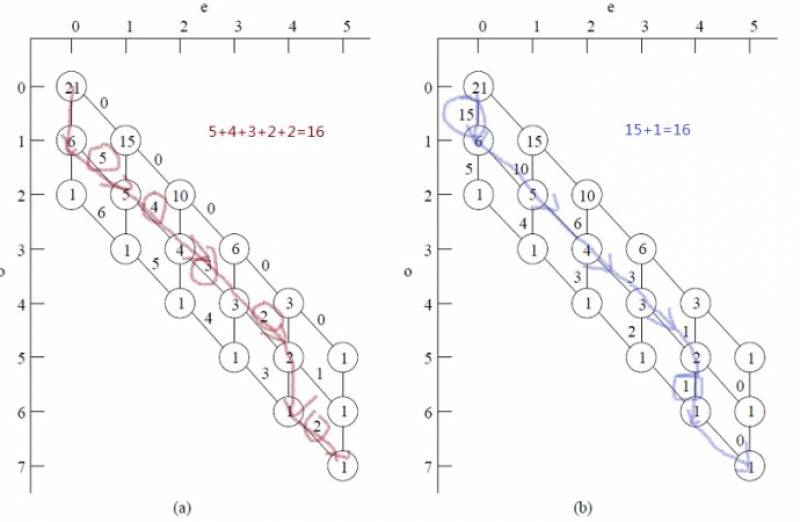
• 5) OK，既然我们已经做出了GUGA的图形。下一步就可以尝试性的“走出”不同的电子组态（行列式）了。a),b)两图中的走法均为|2 3 4 5 7>，DRT（？，待验证）的值均为16。然后，其余的DRT也可以依次走出来。 I_alpha= \sum Y + offset (offset的意思是如果有其他的GUGA图的话，加上前置量)

• 6） 以上只有alpha部分的，beta部分的于此类似，然后构造的DRT表为 DRT（I_alpha,I_beta）的三角形式。此三角形式较方便于进一步的限制和简化。

   PS：最右上的圈数值为21，说明5个alpha电子对应在7个alpha轨道上共有21种排列顺序
      因为是闭壳层体系，beta电子的排列也是只有21种
      我们可以构建出一个21*21的矩阵
      任取上（下）三角，同时包含对角线的元素,即可得到该体系下面所有可能的电子组态（即电子行列式排布）。
      

(J_Sagat)